Figuras y modos en los silogismos.

Un silogismo no es más que una forma de razonamiento deductivo que se compone de 3 elementos básicos: una premisa mayor, una premisa menor y una conclusión que las relaciona.

En la vida diaria utilizamos todo el tiempo esta estructura lógica; sin embargo, donde más se emplea dicho concepto es en el universo de las matemáticas.

Estructura del silogismo

Como ya enunciamos, todo silogismo se estructura sobre la base de dos premisas que son aceptadas como ciertas y una tercera que se deduce lógicamente de la relación entre los conjuntos que se describen en las primeras, y que resulta ser conclusiva. Para entender cómo opera este mecanismo apelemos a un ejemplo clásico:

• Premisa mayor: Una proposición general

             Ej. Todos los hombres son mortales.

• Premisa menor: Una proposición específica

              Ej. Sócrates es un hombre.

• Conclusión: Basada en las dos premisas anteriores

              Ej. Sócrates es mortal.

 

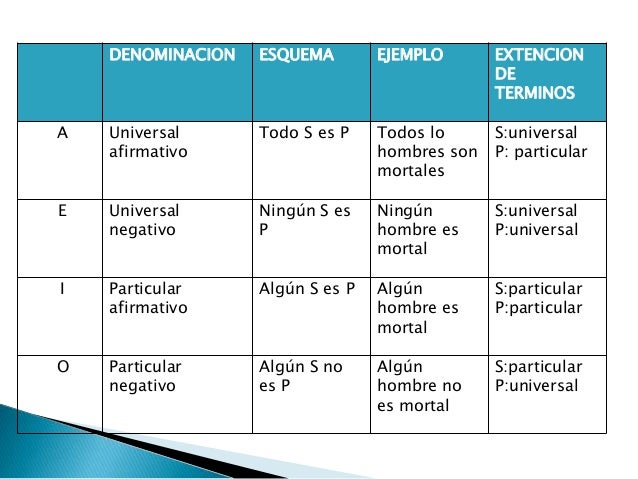
Modo del silogismo es la forma que toma éste de acuerdo con la cantidad y la cualidad de las premisas y la conclusión. De la aplicación de las leyes de los silogismos a los 256 modos posibles resultan válidos solamente 19 y son los que tradicionalmente se memorizan atendiendo a los modos válidos de cada figura con sus premisas y conclusión.

	Así los modos válidos	Se memorizaban cantando
De la primera figura	AAA, EAE, AII, EIO	BARBARA, CELARENT, DARII, FERIO
De la segunda figura	EAE, AEE, EIO, AOO	CESARE, CAMESTRES, FESTINO, BAROCO
De la tercera figura	AAI, IAI, AII, EAO, OAO, EIO	DARAPTI, DISAMIS, DATISI, FELAPTON, BOCARDO, FERISON
De la cuarta figura	AAI, AEE, IAI, EAO, EIO	BAMALIP, CAMENES, DIMATIS, FESAPO, FRESISON

Nota : También son válidos para la primera figura los modos subalternos BARBARI, CELARONT; para la segunda: CESARO, CAMESTROP; y para la cuarta: CAMENOP

Se pueden representar estos modos mediante diagramas de Venn con las siguientes convenciones:

• Cada término del silogismo está representado por S, P, M, por un círculo incoloro que representa a todos los miembros posibles de una clase.
• La conclusión aparece como resultado de la relación de los términos S y P en su relación con M.
• La inexistencia se muestra como zona rellena de color.
• La existencia individual se afirma mediante una X: Al menos uno, o algunos.
• La relación de los términos se constituye como pertenencia o no pertenencia a la clase.
• La relación de inclusión, Todo S es P, se representa como “No hay ningún S que no sea P” según muestra la imagen que se muestra al margen.